この記事では、次の中3数学平方根の問題をちょっぴり自由な方法で解説します。
\(5\sqrt{3}\ \)を\(\ \sqrt{○}\ \) の形に変形しなさい
まずは、この問題を解くのに必要なルールを確認しましょう!
いくら自由といってもルールは決めておかないと考え始められませんからね~
上の2つのルールを使うと
\(5\sqrt{3}\ \)を\(\ \sqrt{?}\ \) の形に変形しなさい
という問題は次のように言い換えられます。
\(5\times\sqrt{3}\ \)は「2乗すると○になる正の数」と表すことができます。
さて、○に入る数は?
では、解説していきます。
\(5\times\sqrt3\ \)を2乗すると何になるかが分かればよいので2乗しましょう。
\(\begin{align*}(5\times\sqrt3)^2&=5\times\sqrt3\times5\times\sqrt3\\&=5\times5\times\sqrt3\times\sqrt3\\&=25\times\textcolor{BrickRed}{\underline{\textcolor{black}{\sqrt3\times\sqrt3}}}\end{align*}\)
ここで赤下線部の\(\sqrt3\times\sqrt3\ \)は何になるのでしょうか?
\(\sqrt{○}\)の決まりを思い出してみましょう。
\(\sqrt3\ \)は2乗して(2回かけて)3になる正の数という意味でした。
だから\(\sqrt3\times\sqrt3\ \)は3になります。
よって
\(25\times\sqrt3\times\sqrt3=25\times3=75\)
です。
つまり\(5\times\sqrt3\ \)は2乗すると75になる正の数だということが分かりました。
そんな数を\(\sqrt75\ \)と表すのでしたね。
よって\(5\sqrt3\ \)は\(\sqrt{75}\ \)と変形できます。
解説は以上です。
この記事ではよくある解法ではないですが、平方根のもともとの意味に基づいて、√の変形を解説しました。
読んでくださった方が「ちょっと平方根の理解が深まった!」と思ってくださったならめちゃくちゃう嬉しいです!
読んでくださりありがとうございました!
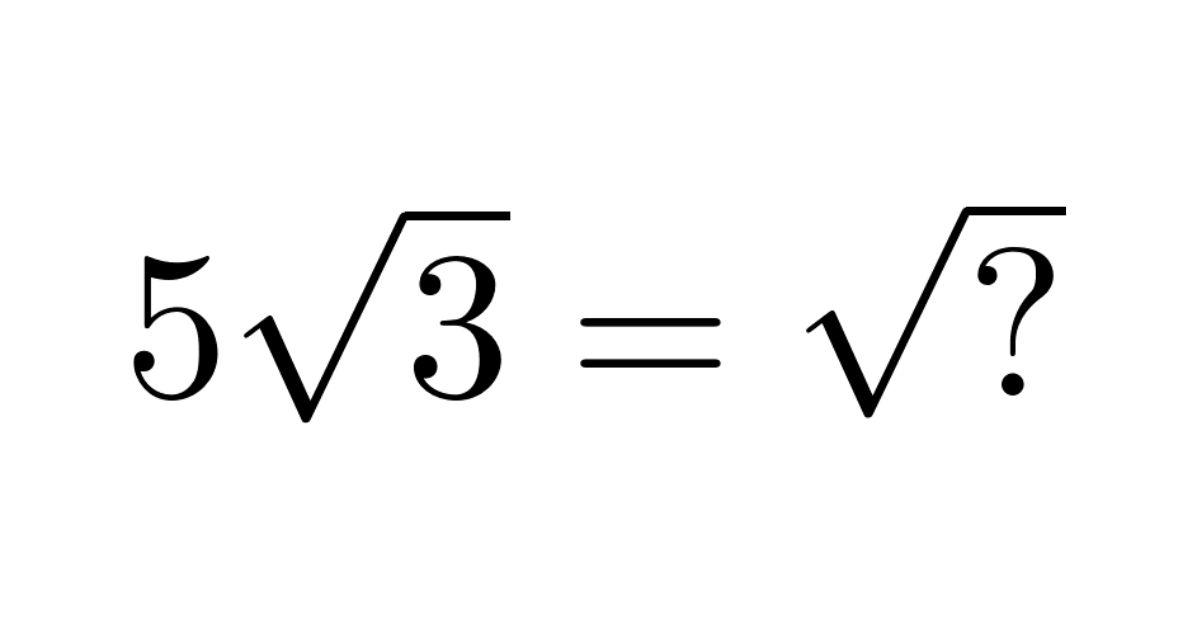
コメント