この記事では小学校算数の次の問題を解説します。
12÷0=?
(とにかく答えを知りたい!という方はここをクリック)
\(12÷0\)を計算しなさいと言われたらどう考えますか?
例えば\(12÷3\)だったら12を3個に分けることだから答えは4。
ということは\(12÷0\)だったら12を0個に分けることだから…無限大??
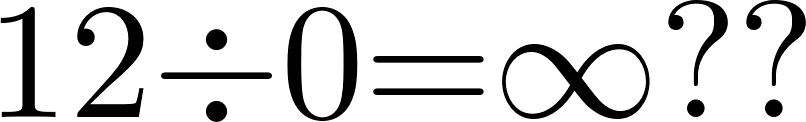
しかし、上に書いたように割り算を「○○個に分けること」と考えるのは欠点があります。
例えば\(12÷\dfrac{1}{3}\)は12を\(\dfrac{1}{3}\)個に分けるという意味になり、「\(\dfrac{1}{3}\)個に分けるってどういうことや?」ってなってしまいます。
そこで、割り算を次のように考えます。
例えば、\(12÷3\)の答えを考えてみましょう。
\(12÷3\)は3をかけて12になる数です。
つまり
\(△\times 3=12\)の△に入る数です。
それは…
4ですね。
だから、\(12÷3=4\)なのです。
では、本題の\(12÷0\)にこの考え方をしてみます。
\(12÷0\)は0をかけて12になる数。
これを数式で表すと
\(△\times 0=12\)の△に入る数は?
これは…
存在しませんね。
どんな数に0をかけても0になってしまうからです。
よって
\(12÷0\)の答えは「存在しない」ということになります。
(正確には\(12÷0\)と表記すること自体がおかしいので、出題者さん、ちゃんとせぇ。という話です。)
ここでちょっと小話です。
では、\(0÷0\)はどうなるのでしょうか。
\(0÷3\)も\(0÷100\)も0です。
だから\(0÷0=0\)なのでしょうか。
あるいは
\(3÷3\)も\(100÷100\)も1です。
だから\(0÷0=1\)なのでしょうか。
これも上と同じように考えてみましょう。
\(0÷0\)は0をかけて0になる数です。
つまり\(△\times0=0\)の△に入る数です。
これは…
無数にあります。
△に5が入っても100が入っても0をかければ0になるからです。
このように、ある数を0で割ることはできないのですが、できない理由が二つあります。
1つ目は答えが存在しないから。((0以外の数)÷0の場合)
2つ目は答えが存在しすぎるから。(\(0÷0\)の場合)
これを最初に学んだとき、「1つの理論で二つの理由が説明できるのかっちょいいな!」と思ったのですが、皆さんはどう思われましたか?
以上です!
読んでいただきありがとうございました!
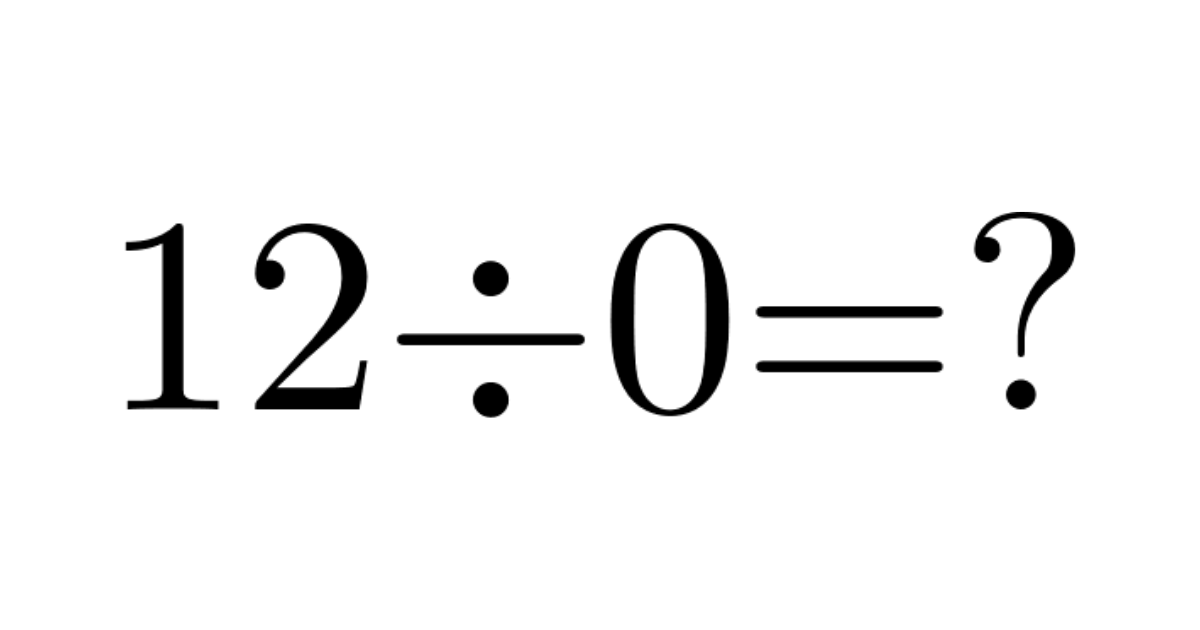
コメント